1. Die Tabelle der Wahrscheinlichkeitsverteilung erinnert an eine Funktionswertetabelle (jeder Wert der ZV kommt ja nur einmal vor). Wir "basteln" uns also eine Funktion $f$, mit den Werten der ZV als Argumente und den zugeordneten Wahrscheinlichkeiten als Werte - das hört sich in Worten komplizierter an als es ist: nehmen wir das Urnenbeispiel der letzten Lektion als Beispiel

   $X$	1	2	3	4	$\Sigma P(X=a_i)$
   $P(X=a_i)$	$\frac{6}{30}$	$\frac{10}{30}$	$\frac{12}{30}$	$\frac{2}{30}$	1

   Hier der Graf dieser Funktion $f$

   

   oder besser

   
   
2. Im obigen Beispiel geben die y-Werte die Wahrscheinlichkeiten an - also je weiter oben ein Punkt desto wahrscheinlicher sein x-Wert. Das ist durchaus eine Möglichkeit der Veranschaulichung bringt uns aber später bei kontinuierlichen ZV nicht mehr weiter. Besser zu verallgemeinern ist ein Ansatz, indem man die Fläche unter der Funktion $f$ verwendet. Das führt uns zu folgender Definition:

3. Die Fläche unter der Funktion im Intervall [a,a+1[ ist gleich der Wahrscheinlichkeit, dass die ZV den Wert a annimmt!
   Um das zu formaliseren brauchen wir eine neue Nomenklatur: Ist $f$ eine positiv definite reelle Funktion, (d.h. $\forall x \in \mathbb{R}: f(x)\ge 0$) dann ist mit $\int \limits_a^b f$ der Flächeninhalt des Graphen im Intervall [a,b] gemeint. Zur Veranschaulichung

   

   Beachte, dass der Flächeninhalt der Recheckflächen leicht auszurechnen ist, da die Breite ja 1 ist, ergibt sie sich einfach als Summe der Wahrscheinlichkeiten: $$\begin{align} P(\Omega) = \int\limits_{-\infty}^{\infty} f = \sum_i P(X=i) = \sum_i p_i = 1 \end{align}$$ $$\begin{align} P(a \leq X \leq b) = \int\limits_{a}^{b+1}\!\!\!\!f = \sum_{i=a}^b P(X=i) \end{align}$$

   

   Bei stetigen ZV wie z.B. Körpergewicht ist es noch leichter: $$\begin{align} P(a \leq X \leq b) = \int\limits_{a}^{b} f \end{align}$$

   Diese wichtige Funktion $f$ heißt Wahrscheinlichkeitsdichte(funktion)

   Der gesamte Flächeninhalt unter einer Wahrscheinlichkeitsdichte ist

   $\int\limits_{-\infty}^{\infty} f =$

   $\forall x \in D_f: f(x) \geq$

   $\int\limits_a^a f =$

4. Bei vielen Beispielen in der Stochastik geht es darum die Dichtefunktion zu bestimmen und damit bestimmte Fragen zu beantworten. Bei diskreter Wertemenge der ZV ist das ja gleichbedeutend mit dem Aufstellen der W-Tabelle aus der vorigen Lektion. Neu ist jetzt
   • die Visualisierung
   • die Möglichkeit zur Verallgemeinerung auf stetige Wertemengen der ZV
   Beispiel: Es wird zweimal gewürfelt. Ist die Ziffernsumme eine Primzahl erhält man den Betrag, ansonsten muss er eingezahlt werden. Wähle eine angemessene ZV, gib deren Verteilung als Tabelle an und gib einen Graf der Dichtefunktion an!

   Wir wählen als ZV X den auszuzahlenden Betrag - er ist negativ, wenn man verliert. Wir schreiben uns die möglichen Werte geordnet in eine Tabelle und überlegen uns deren Wahrscheinlichkeit. (Hier ganzen Bruch in der Schreibweise "x/36" eingeben)

   $X$	-12	-10	-9	-8	-6	-4	2	3	5	7	11	$\Sigma P(X=a_i)$
   $P(X=a_i)$	$\frac{1}{36}$	$\frac{3}{36}$	$\frac{4}{36}$	$\frac{5}{36}$							$\frac{2}{36}$	1

   Die Wahrscheinlichkeitsverteilung (Histogramm) zeichnet man besten mit einem elektronischen Tool wie z.B. 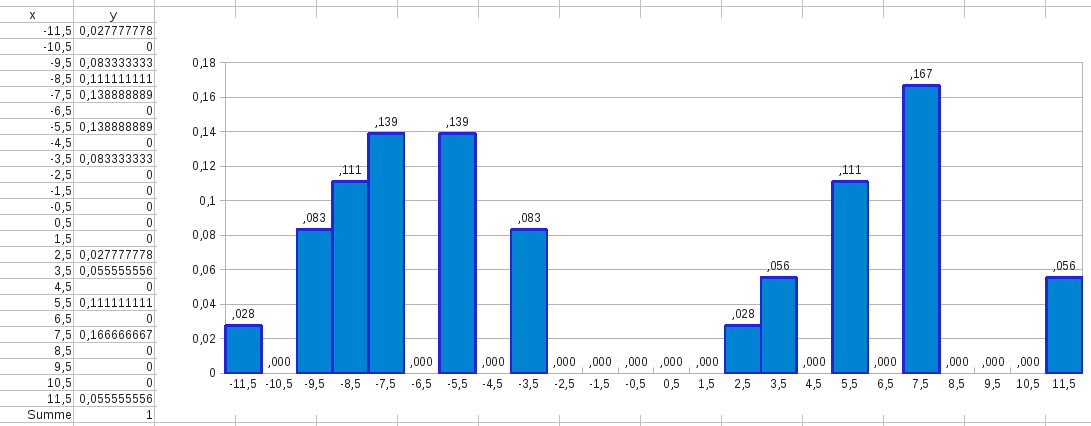LibreOffice Calc (Säulendiagramm, fehlende Werte müssen auf Null gesetzt werden und die Abstände der Säulen muss auf 0% reduziert werden - außerdem scheint es nicht möglich die x-Achsenbeschriftung um eine halbe Einheit zu verschieben, sodass ich als Beschriftung einfach die Intervallmitte gewählt habe) Wer sich das Programm 'gnuplot' installieren möchte, kann sich leicht ein Skript anfertigen, um jedes beliebige Histogramm zu zeichnen und bekommt dies in fast jedem beliebigen Format - ich hab mich hier für SVG(Scalable Vector Graphics) entschieden, weil es von den Browsern unterstützt wird (und wie der Name sagt beliebig skalierbar(vergrößern/verkleinern) ist). Die Bedienung von 'gnuplot' ist wieder eine eigene Geschichte!
   

   

   Skript

   	set terminal svg size 800,300 fname 'Verdana' fsize 8 
   	set output 'boxes.svg'
   	set title "Veranschaulichung einer diskreten ZV mit einem Histogramm"
   	unset key
   	set boxwidth 1 absolute
   	set xtics -12,1,11
   	set grid linetype 5 linecolor rgb "#CCFFFF" linewidth 0.2
   	set style fill solid 0.1 border rgb '#0000ff' 
   	set ylabel "Einheiten in 1/36"
   	plot [-12.5:12.5][0:7]  'die.dat' using ($1+0.5):($2*36) with boxes lc rgb '#C2D6FF' 
   	replot 'die.dat' using ($1+0.5):($2*36+0.5):3 with labels 
   	
   			 	

   Datei: 'die.dat'

   	-12  .02777777777777778 1/36 
   	-10   .08333333333333333 3/36
   	-9   .1111111111111111  4/36
   	-8   .1388888888888889  5/36
   	-6   .1388888888888889  5/36
   	-4   .08333333333333333  3/36
   	2    .02777777777777778  1/36
   	3   .05555555555555555  2/36
   	5   .1111111111111111  4/36
   	7  .1666666666666667  6/36
   	11  .05555555555555555  2/36
   			 		
   			 	

   
   

   
   
   Beantworte an Hand der Tabelle(des Grafen der Dichte folgende Fragen):

   1. Wie groß ist die W. weniger oder gleich 5 Euro zu gewinnen (formal $P(X \leq 5)=$) (Ergebnis in x/36 -- benutze dazu am besten das gnuplot Histogramm, weil das ist in x/36 beschriftet!)
   2. Obige Aufgabe lässt sich als Flächenberechnung unter der Dichte $f$ auffassen: $\displaystyle{ \int\limits_{-\infty}^x f}$.
      Welchen Wert muss $x$ dafür besitzen? (passen Sie auf - "5" ist falsch; Stichwort:"diskrete Verteilung")
   3. Es ist klar: $\displaystyle{ \int\limits_{-\infty}^{a} f + \int\limits_{a}^{\infty} f = 1}$
      Damit lässt sich $\displaystyle{ \int\limits_{-\infty}^{6} f}$ berechnen als $\displaystyle{1 - \int\limits_{x}^{\infty} f}$.
      Wie groß ist $x$?
   4. Bis zu welchem Wert der ZV liegen sie im unteren Quartil (Viertel?)
      (formal $P(X \leq a) \leq 0,25 \quad$ Suche die größte Lösung für $a$ )
   5. Wie groß ist der Erwartungswert $\mu$ auf 2 Dezimalstellen(wxMaxima verwenden)?
   6. Berechne $\sigma = \sqrt{V(X)}$ auf 2 Dezimalstellen}
   7. Wieviel Prozent (gerundet auf Einerstellen) der Ergebnisse liegen innerhalb einer Standardabweichung um den Erwartungswert? (formal $P(\mu - \sigma \leq X \leq \mu + \sigma) = P(|X-\mu|\leq \sigma) = ?$)
   8. Bis zu welchem Wert der ZV liegen sie im oberen Quartil (Viertel?)
      (formal $P(X \geq a) \leq 0,25 \quad$ Suche die kleinste Lösung für $a$ )

5. Wie (beinahe) immer zum Schluss ein kleiner multiple choice Test, um einige Dinge zu wiederholen:

   	Frage	Richtig	Falsch
   1)	Zwischen einer diskreten ZV X und deren Dichtefunktion $f$ besteht folgender Zusammenhang: Seien $a,b$ Werte von X und $a \le b$ $$P(a \leq X \leq b) = \sum_{i=a}^b P(X=i) =\int\limits_a^b f$$	richtig	falsch
   2)	Zwischen einer diskreten ZV X und deren Dichtefunktion $f$ besteht folgender Zusammenhang: Seien $a,b$ Werte von X und $a \le b$ $$P(a \leq X \leq b) = \sum_{i=a}^b P(X=i) =\int\limits_a^{b+1} f$$	richtig	falsch
   3)	Ist nebenstehendes Diagramm eine Wahrscheinlichkeitsdichte?	richtig	falsch

Weiter zu Lektion 4